CÁCH TÍNH LIM (giới hạn) BẰNG CASIO/VINACAL FX 570 ESCÁCH NHÂN ĐA THỨC CHỈ BẰNG MÁY TÍNHKhai triển đa thức có chứa tham số m bằng số phức (anh Mẫn Tiệp)KIỂM TRA TÍNH ĐỒNG BIẾN NGHỊCH BIẾN CỦA HÀM SỐ, NHẨM NGHIỆM NGUYÊN CỦA PHƯƠNG TRÌNH CÁCH TÍNH PHƯƠNG TRÌNH BẬC HAI CHỨA CĂN CASIO FX 570 ESTÍNH UCLN BCNN hai số A,BKIỂM TRA XEM MỘT SỐ CÓ PHẢI LÀ SỐ NGUYÊN TỐ HAY KHÔNG?TÌM CĂN BẬC HAI SỐ PHỨCGIẢI NHANH SƠ ĐỒ CHÉO HOÁ HỌC
CÁCH TÍNH LIM (giới hạn) BẰNG CASIO FX 570 ES
I) tính lim x -> + 1: nhập biểu thức cần tính lim, ví dụ:

2: Ấn CALC3: Nhập một số thật lớn (vì x tiến s về +), ví dụ 9 x10 9, 9999999,98989898,…
Đang xem: Cách tính lim bằng máy tính fx 570es plus
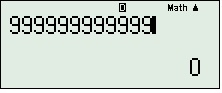
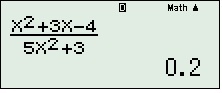
5: lấy kết quả “đẹp” (ở đây là 0.2), ví dụ: nếu nó ra 0,99999999999 thì bạn lấy kết quả là 1, 1,333334–>1,333333–>

6: nếu kết quả là số rất lớn (985764765, 36748968,1.2534×10^28,…) hoặc rất bé(-846232156,..), đừng sợ, đó là +vô cùng (và – vô cùng) đó!II) Tính lim x-> –tương tự bên trên, thêm dấu trừ ví dụ: -9×10 9, -999999999, -88888888,…III) Tính

ví dụ:

1, nhập biểu thức


2, Ấn CALC3, bấm 1+ (vì tiến về 1+)4, nhập <1>
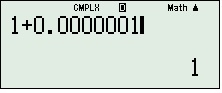
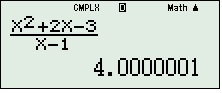
6, lấy kết quả “đẹp” (ở đây là bằng 4), ví dụ: nếu nó ra 0,99999999999 thì bạn lấy kết quả là 1, 1,333334–>1,333333–>

nếu kết quả là số rất lớn (985764765, 36748968,1.2534×10^28…) hoặc rất bé(-846232156,..), đừng sợ, đó là + (và -) đó!Nếu kết quả có dạng

, ví dụ: 5.12368547251.10^-25, nghĩa là 0,000…00512… (gần về 0), kết quả là 0

IV) Tính

tương tự, đổi 1+ thành 1-*) VÍ DỤ ÁP DỤNG:tính

, ta bấm

,bấm CALC, bấm 2+ (vì đề chỉ cho tiến về 2 nên ta tạm cho nó về 2+ trước), bấm <1>

, ta bấm

, bấm CALC, bấm <9>
CÁCH NHÂN, CHIA ĐA THỨC CHỈ BẰNG MÁY TÍNH
(Rút gọn biểu thức bằng máy tính :D)
(nhanh hơn cách dùng hoocne)
Phương pháp này mình nghĩ ra năm lớp 10 và thấy khá hữu ích trong áp dụng giải đề thi đại học, mình muốn chia sẻ với mọi người và hy vọng giúp đỡ được các bạn phần nào trong đề thi đại học 🙂 Ở Việt Nam, đây là trang web đầu tiên đăng tải phương pháp bấm máy này. Bạn nào nếu có ý tưởng phát triển thêm này thì cứ liên hệ mình qua Face nha, có gì mình cùng hợp tác nghiên cứuNếu các bạn đã xem một số bài viết được viết lại tương tự ở một trang nào khác thì cũng nên đọc bài viết của mình để được cập nhật chính xác và đầy đủ nhất về phương pháp bấm máy sau đây. (Ví dụ như vì sao nên dùng 1000 thay vì 100 trong quá trình tính toán, vân vân và vân vân…) Mời các bạn đến với bài viết:* CHÚ Ý: CÁC BẠN PHẢI LÀM HẾT TẤT CẢ CÁC VÍ DỤ NÀY ĐỂ HIỂU RÕ CÁCH LÀM NÀYa) Đối với máy Fx 570MS, 570ES, 570ES PLUS, 570VN PLUS
Hehe! Có bao giờ bạn nghĩ rằng bạn có thể nhân những đa thức loằng ngoằng phức tạp bằng cách chỉ sử dụng máy tính không?Ví dụ:(x+1)(x+2)+(3×2+x+6)(x+7), bạn giải ra kết quả là 3×3+23×2+16x+44
Máy hiện 3023016044, bạn tách chúng thành từng cụm ba chữ số 3,023,016,044 (nhớ là từ tách bên phải sang nghe), và đó chính là các hệ số cần tìm 3,23,16,44. Ta viết 3×3+23×2+16x+44
Đã có kết quả! Nhưng bắt buộc phải thử lại bằng cách bấm qua trái, bấm thêm –(3X3+23X2+16X+44) CALC 7 =, máy báo bằng 0, phép tính mình đúng
Xin giải thích một chút về quy trình bấm phím: bạn bấm 1000 <=> cho mọi bài toán,khi nhập phép tính thay x bằng Ans
Lần này phải cẩn thận hơn! Ở nhóm 957 ta hiểu là -43 (vì 1000-957=43) chứ không phải 957! Vì sao ư? Đơn giản là vì 957 là số quá lớn không thể là hệ số của phép nhân này được và ta phải lấy 1000 trừ cho nhóm đó
Dấu hiệu cần chú ý tiếp theo là nhóm 026, nhóm này đứng sau nó là nhóm 957 (nhóm có hệ số âm), vậy ta lấy 26+1=27, hiểu đơn giản đằng sau nhóm có hệ số âm thì phải nhớ 1 (như kiểu học cấp 1 ý hihi)
Tóm lại, các hệ số cần tìm 5,27,-43,0 biểu thức cần tìm là 5×3+27×2-43x. Ta BẮT BUỘC thử lại bằng cách qua trái, bấm thêm -(5X3+27X2-43X) CALC 7 = máy báo bằng 0 nghĩa là đúng
Máy hiện 999001014 tách thành 0,999,001,014 các hệ số lần lượt là 1,-1,1,14. Kết quả x3-x2+x+14. Ta thử lại bằng cách bấm qua trái, bấm thêm -(X3-X2+X+14) CALC 7 = máy báo bằng không nghĩa là đúng
Ví dụ 4:(x2-3x-7)(x+2) bạn bấm (X2-3X-7)(X+2) CALC 1000 <=>, máy hiện 998986986, tách thành 0,998,986,986. Bài này ta phân tích từ phải qua như sau 986 thành -14, tiếp theo 986 nhớ 1 là 987 rồi thành -13, tiếp theo 998 nhớ 1 là 999 rồi thành -1các hệ số ta suy ra 1,-1,-13,-14 ta có kết quả x3-x2-13x-14. Ta thử lại bằng cách qua trái, bấm -(X3-X2-13X-14) CALC 7 = máy báo bằng 0 nghĩa là đúngVí dụ 5:(x+5)(x+3)(x-7)-(4×2-3x+7)(x-1) làm tương tự, máy hiện -2992051098, ta có các hệ số 3,-8,51,98. Ta coi dấu trừ ở dãy số hiện ra là dấu trừ cho toàn bộ biểu thức. Vậy kết quả là -(3×3-8×2+51x+98)= -3×3+8×2-51x-98. Ta thử lại bằng cách qua trái, bấm -(-3X3+8X2-51X-98) CALC 7 = máy báo bằng 0 nghĩa là đúngVí dụ 6:(x2+3x+2)(5-3x)-(x+2)(x-1)-(2x+3)(x-1)Đến bài này mình xin trình bày luôn cách dùng nháp kết hợp nhẩm sao cho có hiệu quả, giúp các bạn tự tin hơn trong việc vận dụng làm toánBạn làm tương tự như các bài trên, máy hiện -3006992985. Chuẩn bị 1 tờ giấy nháp và viết vào nháp các hệ số từ phải sang lần lượt như saulần 1 -15lần 2 -7 -15lần 3 7 -7 -15lần 4 3 7 -7 -15lần 5 -3 -7 +7 +15 (vì có dấu trừ ở đầu)thử lại bằng cách qua trái -(-3X3-7X2+7X+15) CALC 7 = máy báo bằng 0 nghĩa là kết quả đúngGhi vào bài làm chính thức kết quả -3×3-7×2+7x+15Ví dụ 7,8,9:(tự luyện)(-5×2+3x-2)(x+1)+5x-7 = -5×3-2×2+6x-9(2×2+3x-7)(x-3)+(2-x)(x+1)(x-3) = x3+x2-17x+15×3+5x-7+(x2+3)(x-4) = 2×3-4×2+8x-19Ví dụ chia đa thức:* Thông thường chia đa thức người ta thường dùng cách chia được dùng năm lớp 8 hoặc nếu chia không dư ta có thể dùng phương pháp chia hoocne (horner). Nhưng với phương pháp này ta có thể dùng để chia đa thức ko dư mà không cần dùng đến hoocne (horner).Nếu bạn hiểu cách nhân đa thức rồi thì chỉ cần thay nhân bằng chia là đượcbài toán (2×3-3×2-16x+21)/(x-3) ta bấm tương tự như nhân đa thức ra kết quả 2002993, vậy kết quả là 2×2+3x-7Cách này dù không chia có dư được nhưng lại rất có giá trị trong việc nhẩm nghiệm phương trình bậc 3 hoặc bậc 4Ví dụ: x^3+4x^2-3x-2=0Bấm máy ra một nghiệm chẳn x=1 và hai nghiệm lẻchia (x^3+4x^2-3x-2) cho (x-1) ra x^2+5x+2giải tiếp phương trình trênx^2+5x+2=0 ra hai nghiệm lẻ còn lại là (-5+ căn 17)/2 và (-5-căn 17)/2xong!* Chia đa thức có dư trên máy VINACAL fx570es plus với tính năng Q…rCác bạn bấm 1000= Shift VINACAL 1 sau đó nhập tử số Shift ) sau đó nhập mẫu số. Kết quả sẽ cho ra Q= kết quả R= số dư* Chia đa thức có dư trên máy CASIO fx570VN plus với tính năng÷RVí dụ (2×3-3×2-15x+23)/(x-3)Ta giải tay bài này như sau:2×3-3×2-15x+23=2×3-6×2+3×2-9x-6x+18+5=2×2(x-3)+3x(x-3)-6(x-3)+5=(2×2+3x-6)(x-3)+5Kết quả 2×2+3x-6 dư 5Giải máyCác bạn nhập (2×3-3×2-15x+23) Alpha Phân số (x-3) CALC 1000 <=>Kết quả sẽ cho ra 2002994 , R=5Nghĩa là kết quả 2×2+3x-6 dư 5Ta thử lại bằng cách (2X2+3X-6)(X-3) CALC 1000 <=>Kết quả 1996985018, nghĩa là 2×3-3×2-15x+18 (vì có dư 5) vậy là phép tính đúng.
Xem thêm: Đội Bóng Thiếu Lâm – Em Cua Ngay Hom Qua Doi Bong Thieu Lam
Bản chất: Hy vọng qua những ví dụ cụ thể trên các bạn có thể cơ bản nắm được bản chất của phương pháp này. Bản chất chỉ là thế giá trị 1000 vào tất cả các giá trị x để tính toán thôi. Mặc dù rất đơn giản nhưng rất có ích không phải ai cũng biết.
Xem thêm: Hướng Dẫn Cách Nhận Biết Iphone 5 Lock Và Quốc Tế, Hướng Dẫn Cách Nhận Biết Iphone 5S Bản Quốc Tế
Ưu điểm của phương pháp: nhanh, ra kết quả có độ chính xác cao (hơn giải tay rất nhiều)Hầu hết đề thi bậc phổ thông đều không có hệ số quá phức tạp nên áp dụng cách này rất hữu hiệu!
Lưu ý: Mình có một yêucầu thế này, trong mọi bài toán bước thử lại là không thể bỏ qua. Bước thử lạigần như là linh hồn của phương pháp này. Nó không mất của bạn quá vài giây, nhưng nếu bạn ko làm thì phương pháp này trở thành con dao hai lưỡi giết chếtbạn. Nếu bạn thử lại ở mọi bài toán, bạnsẽ không còn hoài nghi gì về kết quả hay phương pháp mình làm đúng hay sai nữa.Nhờ việc thử lại những bước trước bạn có thể tự tin nhẩm mà không sợ sau này kếtquả sai. Theo kinh nghiệm của mình, khi bạn đã thuần thục phương pháp này, thờigian bạn hoàn thành một phép tính bao gồm cả thử lại chỉ 5 giây, thậm chí vớinhững bài toán đơn giản áp dụng phương pháp này vẫn rất nhanh (cái này gọi làphụ thuộc máy tính đó, hehe). Phương pháp này mình nghĩ ra từ hè 11 lên 12,mình có cả năm 12 để rèn luyện để tìm ra ưu nhược điểm của phương pháp, và mìnhkết luận bước thử lại là quan trọng nhất. Nó đem lại một ưu điểm mà phương phápgiải tay không bao giờ đem lại được, đó là tính chính xác. Nhiều khi vì sựchính xác này đến cả những bài đơn giản như (x+1)(x+2) cũng có thể bấm máy, vìbiết đâu nếu mình giải tay thì sai bước nào đó thì sao.Ngoài ra, bước nhập biểu thức ban đầu, sau khi nhập xong bạn nên dùng con trỏ rà lại để đảm bảo mình nhập đúng. Nếu bạn làm đúng thì không sợ gì kết quả sai nữa
Thêm một lưu ýnữa là nhớ mở ngoặc thì phải đóng ngoặc. Việc mở ngoặc đóng ngoặc bậy bạ cũnglà một nguyên nhân gây sai kết quả. Nhưng thường sau khi thử lại bạn sẽ nhìn rađiểm sai của mình để sửa nên ko sao
Trong một sốtrường hợp bạn thử lại kết quả vẫn sai thì bạn nên chuyển sang giải taycho kịp giờ. Còn nếu lúc rảnh rỗi thì bạn cố gắng kiểm tra xem mình sai ở bướcnào, từ đó rút được kinh nghiệm.Trong trường hợp hệ số là phân số thì phương pháp này không đúng, trường hợp này ta nên chuyển về số nguyên để tính toán cho thuận tiện
Phương pháp bấmmáy này mình đã vận dụng vào kì thi đại học rất thành công. Ở môn toán, gần nhưko có bài nào là mình không áp dụng, nó đã hạn chế sai sót của mình rất nhiều. Mình muốn khẳng định rằng phương phápnày cực kì có ý nghĩa trong đề thi đại học.Tại sao không phải 100 mà là 1000?Cài này nhiều bạn thắc mắc. Dĩ nhiên là thế 1000 hay 100 đều giống nhau, chỉ cần thay vì nhóm 3 chữ số thì chuyển sang nhóm 2 chữ số thôi. Nhưng qua quá trình làm toán mình xin khẳng định là không nên dùng 100. Vì chọn 100 giúp ta làm gọn kết quả trên màn hình và có thể tính toán lên đến bậc 4 (thậm chí bậc 5) nhưng lại rất dễ sai ở các hệ số từ 25 trở lên (có lúc hệ số dưới 10 mà vẫn sai). Với 1000 thì mọi hệ số có 2 chữ số đều đảm bảo đúng (khoảng dưới 200 vẫn đúng). Qua quá trình học 12 ôn thi đại học, rất ít trường hợp tính toán bậc 4 nhưng lại rất nhiều trường hợp hệ số đạt đến 50 (rất nhiều lần là hơn 100). Lúc đó, nếu áp dụng 100 thì lúc bạn thử lại kết quả sẽ là sai và bạn phải chuyển sang 1000 mới có kết quả đúng. Mình cũng không cứng nhắc bắt các bạn chọn 1000 vì có nhiều khi sử dụng song song rất có hiệu quả. (Nhưng ít lắm)