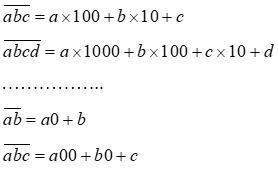Home / Tin Tức / Tóm Tắt Công Thức Toán Học Lớp 4 Và 5 Theo Chủ Đề Tóm Tắt Công Thức Toán Học Lớp 4 Và 5 Theo Chủ Đề 06/04/2022 Lớp 1 Lớp 2 Lớp 2 - kết nối tri thức Lớp 2 - Chân trời sáng sủa tạo Lớp 2 - Cánh diều Tài liệu tham khảo Lớp 3 Sách giáo khoa Tài liệu tham khảo Sách VNEN Lớp 4 Sách giáo khoa Sách/Vở bài tập Đề thi Lớp 5 Sách giáo khoa Sách/Vở bài bác tập Đề thi Lớp 6 Lớp 6 - kết nối tri thức Lớp 6 - Chân trời sáng tạo Lớp 6 - Cánh diều Sách/Vở bài xích tập Đề thi Chuyên đề & Trắc nghiệm Lớp 7 Sách giáo khoa Sách/Vở bài bác tập Đề thi Chuyên đề và Trắc nghiệm Lớp 8 Sách giáo khoa Sách/Vở bài bác tập Đề thi Chuyên đề và Trắc nghiệm Lớp 9 Sách giáo khoa Sách/Vở bài bác tập Đề thi Chuyên đề & Trắc nghiệm Lớp 10 Sách giáo khoa Sách/Vở bài bác tập Đề thi Chuyên đề & Trắc nghiệm Lớp 11 Sách giáo khoa Sách/Vở bài xích tập Đề thi Chuyên đề và Trắc nghiệm Lớp 12 Sách giáo khoa Sách/Vở bài tập Đề thi Chuyên đề & Trắc nghiệm IT Ngữ pháp giờ Anh Lập trình Java Phát triển web Lập trình C, C++, Python Cơ sở dữ liệu Công thức, Định nghĩa Toán, Lí, HóaĐường thẳngHình tam giácCác trường phù hợp tam giác bằng nhauHình thangHình bình hànhHình thoiHình chữ nhậtTổng hợp kiến thức cơ bản Toán lớp 4 học tập kì 1, học kì 2 đưa ra tiếtTải xuốngSỐ TỰ NHIÊN1. Số với chữ số - sử dụng 10 chữ số để viết số là: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ● tất cả 10 số có 1 chữ số (từ 0 mang lại 9) ● tất cả 90 số có 2 chữ số (từ 10 mang lại 99) ● bao gồm 900 số tất cả 3 chữ số (từ 100 mang đến 999) ● có 9000 số có 4 chữ số (từ 1000 mang lại 9999)- Số tự nhiên nhỏ nhất là số 0. Không tồn tại số tự nhiên lớn nhất.Bạn đang xem: Tóm Tắt Công Thức Toán Học Lớp 4 Và 5 Theo Chủ Đề- nhì số trường đoản cú nhiên liên tiếp hơn (kém) nhau một 1-1 vị.- những số có chữ số tận cùng là 0, 2, 4, 6, 8 gọi là số chẵn. Nhì số chẵn liên tiếp hơn hèn nhau 2 đơn vị.- các số bao gồm chữ số tận thuộc là 1, 3, 5, 7, 9 gọi là số lẻ. Nhì số lẻ liên tục hơn hèn nhau 2 đối chọi vị.2. Hàng và lớp* Lớp nghìnSốLớp nghìnLớp 1-1 vịTrăm nghìnChục nghìnNghìnTrămChụcĐơn vị56756734 56734567234 567234567Hàng đối kháng vị, sản phẩm chục, hàng nghìn hợp thành lớp đối kháng vị.Hàng nghìn, hàng chục nghìn, hàng trăm ngàn hợp thành lớp nghìn.3. Triệu với lớp triệuSốLớp triệuLớp nghìnLớp đối chọi vịTrăm triệuChục triệuTriệuTrăm nghìnChục nghìnNghìnTrămChụcĐơn vị123 456 789123456789BIỂU THỨCA. Những loại biểu thức thường gặp1. Biểu thức bao gồm chứa một chữVí dụ: 3 + a là biểu thức bao gồm chứa một chữ+ ví như a = 1 thì 3 + a = 3 + 1 = 4; 4 là cực hiếm của biểu thức 3 + a+ ví như a = 2 thì 3 + a = 3 + 2 = 5; 5 là giá trị của biểu thức 3 + a+ nếu như a = 3 thì 3 + a = 3 + 3 = 6; 6 là giá trị của biểu thức 3 + a2. Biểu thức có chứa hai chữVí dụ: a + b là biểu thức bao gồm chứa hai chữ+ ví như a = 3 với b = 2 thì a + b = 3 + 2 = 5; 5 là cực hiếm của biểu thức a + b+ ví như a = 4 cùng b = 0 thì a + b = 4 + 0 = 4; 4 là quý hiếm của biểu thức a + b+ giả dụ a = 0 với b = 1 thì a + b = 0 + 1 = 1; một là giá trị của biểu thức a + bMỗi lần vắt chữ số bằng số ta tính được một quý giá của biểu thức a + b.3. Biểu thức gồm chứa tía chữVí dụ: a + b + c là biểu thức gồm chứa tía chữ+ trường hợp a = 2, b = 3 cùng c = 4 thì a + b + c = 2 + 3 + 4 = 5 + 4 = 9+ nếu a = 5, b = 1 với c = 0 thì a + b + c = 5 + 1 + 0 = 6 + 0 = 6+ giả dụ a = 1, b = 0 và c = 2 thì a + b + c = 1 + 0 + 2 = 1 + 2 = 3B. Phương pháp tính giá trị của biểu thức 1. Biểu thức không tồn tại dấu ngoặc 1-1 chỉ có phép cộng và phép trừ (hoặc chỉ gồm phép nhân với phép chia) thì ta tiến hành các phép tính theo trang bị tự trường đoản cú trái sang phải.Ví dụ:a) 542 + 123 – 79 = 665 – 79 = 586 b) 482 × 2 : 4 = 964 : 4 = 2412. Biểu thức không có dấu ngoặc đơn, có các phép tính cộng, trừ, nhân, phân tách thì ta triển khai các phép tính nhân, phân tách trước rồi thực hiện các phép tính cùng trừ sau.Ví dụ: 27 : 3 - 4 × 2 = 9 - 8 = 13. Biểu thức gồm dấu ngoặc đơn thì ta thực hiện các phép tính trong ngoặc đối kháng trước, các phép tính ngoại trừ dấu ngoặc đối kháng sau.Ví dụ: 25 × (21 + 120) = 25 × 141 = 3525BỐN PHÉP TÍNH VỚI SỐ TỰ NHIÊNA. PHÉP CỘNG1. đặc điểm giao hoána + b = b + aVí dụ: 2 + 3 = 3 + 22. Tính chất phối kết hợp của phép cộng(a + b) + c = a + (b + c)Ví dụ: (2 + 3) + 4 = 2 + (3 + 4)3. Cộng với 00 + a = a + 0 = aVí dụ: 0 + 9 = 9 + 0Nhận xét:+ trong một tổng có con số các số hạng lẻ là lẻ thì tổng kia là một vài lẻ.+ trong một tổng có số lượng các số hạng lẻ là chẵn thì tổng kia là một số chẵn.+ Tổng của những số chẵn là một trong những chẵn.+ Tổng của một số lẻ và một số trong những chẵn là một số trong những lẻ.+ Tổng của hai số trường đoản cú nhiên liên tục là một số trong những lẻ.B. PHÉP TRỪ1. a - (b + c) = (a - c) - b = (a - b) - c2. Nếu số bị trừ và số trừ cùng tăng (hoặc giảm) n đơn vị chức năng thì hiệu của chúng không đổi.3. Nếu số bị trừ được vội lên n lần và không thay đổi số trừ thì hiệu được tăng thêm một số trong những đúng bằng (n - 1) lần số bị trừ (n > 1).4. Nếu số bị trừ giữ nguyên, số trừ được gấp lên n lần thì hiệu bị giảm xuống (n - 1) lần số trừ (n > 1).5. Nếu số bị trừ được tăng thêm n 1-1 vị, số trừ không thay đổi thì hiệu tăng thêm n đối chọi vị.6. Nếu số bị trừ tăng thêm n solo vị, số trừ giữ nguyên thì hiệu giảm sút n đối kháng vị.C. PHÉP NHÂN1. Tính hóa học giao hoána × b = b × aVí dụ: 2 × 3 = 3 × 22. Tính chất kết hợpa × (b × c) = (a × b) × cVí dụ: 2 × (3 × 4) = (2 × 3) × 43. Nhân cùng với 0a × 0 = 0 × a = 0Ví dụ: 2 × 0 = 0 × 2 = 04. Nhân cùng với 1a × 1 = 1 × a = aVí dụ: 4 × 1 = 1 × 4 = 45. Tính chất phân phối của phép nhân với phép cộnga × (b + c) = a × b + a × cVí dụ: 3 × (2 + 3) = 3 × 2 + 3 × 36. tính chất phân phối của phép nhân với phép trừa × (b - c) = a × b - a × cVí dụ: 6 × (9 – 3) = 6 × 9 – 6 × 37. vào một tích giả dụ một vượt số được vội lên n lần đồng thời tất cả một quá số không giống bị giảm đi n lần thì tích không vậy đổi.8. trong một tích tất cả một vượt số được cấp lên n lần, những thừa số còn lại giữ nguyên thì tích được vội vàng lên n lần và trái lại nếu trong một tích bao gồm một quá số bị giảm đi n lần, các thừa số còn lại giữ nguyên thì tích cũng trở nên giảm đi n lần. (n > 0)9. Trong một tích, giả dụ một quá số được vội vàng lên n lần, bên cạnh đó một thừa số được gấp lên m lần thì tích được vội vàng lên (m × n) lần. Ngược lại nếu vào một tích một thừa số bị giảm đi m lần, một vượt số bị giảm xuống n lần thì tích bị giảm đi (m × n) lần (m cùng n không giống 0).10. Trong một tích, ví như một quá số được tạo thêm a đối chọi vị, các thừa số còn lại không thay đổi thì tích được tăng lên a lần tích các thừa số còn lại.11.Xem thêm: Xem Danh Sách Trúng Tuyển Đại Học Ở Đâu ? Kiểm Tra Thí Sinh trong một tích, trường hợp có ít nhất một quá số chẵn thì tích kia chẵn.12. Trong một tích, nếu như có tối thiểu một vượt số tròn chục hoặc ít nhất một thừa số gồm tận cùng là 5 với có ít nhất một quá số chẵn thì tích tất cả tận thuộc là 0.13. Trong một tích các thừa số đa số lẻ và có tối thiểu một vượt số có tận cùng là 5 thì tích tất cả tận thuộc là 5.D. PHÉP CHIA1. a : (b × c) = a : b : c = a : c : b (b, c > 0)2. 0 : a = 0 (a > 0)3. a : c - b : c = ( a - b) : c (c > 0)4. a : c + b : c = (a + b) : c (c > 0)5. Trong phép chia, ví như số bị chia tăng thêm (giảm đi) n lần (n > 0) đồng thời số chia giữ nguyên thì yêu mến cũng tạo thêm (giảm đi) n lần.6. Trong một phép chia, giả dụ tăng số phân chia lên n lần (n > 0) bên cạnh đó số bị chia không thay đổi thì thương giảm xuống n lần với ngược lại.7. trong một phép chia, trường hợp cả số bị chia và số chia mọi cùng vội vàng (giảm) n lần (n > 0) thì yêu đương không ráng đổi.8. vào một phép chia gồm dư, ví như số bị phân chia và số phân chia cùng được cấp (giảm) n lần (n > 0) thì số dư cũng khá được gấp (giảm) n lần.DÃY SỐ1. Đối cùng với số tự nhiên và thoải mái liên tiếpa) hàng số thoải mái và tự nhiên liên tiếp ban đầu là số chẵn dứt là số lẻ hoặc bước đầu là số lẻ và xong bằng số chẵn thì số lượng số chẵn bằng con số số lẻ.b) hàng số tự nhiên liên tiếp bắt đầu bằng số chẵn và chấm dứt bằng số chẵn thì số lượng số chẵn nhiều hơn thế số lượng số lẻ là 1.c) dãy số thoải mái và tự nhiên liên tiếp bắt đầu bằng số lẻ và xong bằng số lẻ thì số lượng số lẻ nhiều hơn thế số lượng số chẵn là 1.2. Một số quy vẻ ngoài của hàng số thường gặpa) từng số hạng (kể trường đoản cú số hạng lắp thêm 2) thông qua số hạng đứng tức thời trước nó cùng hoặc trừ một số trong những tự nhiên.Ví dụ: 2, 5, 8, 11, …Dãy số bên trên được viết theo quy luật: Số hạng đứng ngay thức thì sau ngay số hạng đứng tức thì trước cộng với 3.b) từng số hạng (kể từ bỏ số hạng vật dụng 2) thông qua số hạng đứng tức thời trước nó nhân hoặc chia một trong những tự nhiên.Ví dụ: 1024, 512, 256, 128, …Dãy số bên trên được viết theo quy luật: Số hạng đứng lập tức sau thông qua số hạng đứng liền trước chia cho 2.c) mỗi số hạng (kể từ bỏ số hạng máy 3) bằng tổng nhị số hạng đứng ngay tức khắc trước nó.Ví dụ: 1, 2, 3, 5, 8, 13, 21,…Dãy số được viết theo quy luật: trường đoản cú số hạng lắp thêm ba, số hạng đứng sau bởi tổng hai số hạng đứng ngay tức thì trước nó (3 = 2 + 1, 5 = 3 + 2, 8 = 5 + 3, ….)3. Hàng số giải pháp đều*) kiếm tìm số số hạng của hàng số cách đềuSố số hạng = (Số cuối – Số đầu) : khoảng cách giữa nhì số hạng thường xuyên + 1Ví dụ. tìm kiếm số số hạng của dãy số: 1, 4, 7, 10, 13, 16, 19, …, 94, 97, 100Bài giảiSố số hạng của dãy số đã đến là:(100 – 1) : 3 + 1 = 34 (số hạng)Đáp số: 34 số hạng*) Tính tổng của dãy số cách đềuTổng = (Số đầu + Số cuối) × Số số hạng : 2Ví dụ. Tính tổng của dãy số: 1, 4, 7, 10, 13, 16, 19, …, 94, 97, 100Bài giảiSố số hạng của hàng số bên trên là: 34 số hạngTổng của dãy số trên là:(100 + 1) × 34 : 2 = 1717Đáp số: 1717DẤU HIỆU phân tách HẾT1. Tín hiệu chia hết đến 2Các số có chữ số tận cùng là 0, 2, 4, 6, 8 thì chia hết đến 2.Ví dụ:12, 14, 16, 18 là hầu như số phân chia hết mang đến 2 vì bao gồm chữ số tận cùng là 2, 4, 6, 811, 13, 15, 17 là những số không phân chia hết cho 2 vì bao gồm chữ số tận cùng là 1, 3, 5, 7- Số chia hết cho 2 là số chẵn.- Số không phân chia hết đến 2 là số lẻ.2. Dấu hiệu chia hết mang đến 5Các số gồm chữ số tận cùng là 0 hoặc 5 thì chia hết đến 5.Ví dụ:945, 3000 là mọi số chia hết cho 5 bởi số đó tất cả chữ số tận thuộc lần lượt là 5, 010, 25 là đa số số phân chia hết cho 5 vì chưng những số đó tất cả tận thuộc là 0, 53. Tín hiệu chia hết cho 9Các số bao gồm tổng các chữ số phân chia hết cho 9 thì phân chia hết mang đến 9.Các số có tổng các chữ số không chia hết cho 9 thì không phân chia hết mang lại 9.Ví dụ:a) 657 : 9 = 73Ta có:6 + 5 + 7 = 1818 : 9 = 2b) 451 : 9 = 50 (dư 1)Ta có:4 + 5 + 1 = 1010 : 9 = 1 (dư 1)4. Dấu hiệu chia hết đến 3Các số có tổng những chữ số phân tách hết mang đến 3 thì phân chia hết mang đến 3.Các số tất cả tổng các chữ số không phân tách hết mang đến 3 thì không phân chia hết đến 3.Ví dụ:a) 63 : 3 = 21Ta có:6 + 3 = 99 : 3 = 3b) 125 : 3 = 41 (dư 2)Ta có:1 + 2 + 5 = 88 : 3 = 2 (dư 2)CẤU TẠO SỐSử dụng kết cấu số:Ví dụ: cho số có 2 chữ số, nếu rước tổng những chữ số cùng với tích những chữ số của số đã cho thì bằng chính số đó. Tìm chữ số hàng đơn vị chức năng của số sẽ cho.
